Mathematics desk
< December 7	<< Nov \| December \| Jan >>	December 9 >

Welcome to the Wikipedia Mathematics Reference Desk Archives
The page you are currently viewing is an archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages.

December 8[edit]

Artin–Schreier theory[edit]

Are polynomials of the form ${\frac {x^{6k+2}-x+1}{x^{2}-x+1}}$ always irreducible over the rationals ? It seems to be true for $k\leq 100.$ Is this perhaps an open question ? If not, are there any known counter-examples, or -on the contrary- proofs of its irreducibility ? — 79.118.185.225 (talk) 04:57, 8 December 2014 (UTC)[reply]

I don't know the answer (I believe it to be yes), but presumably it is useful to observe that the zeros of

p_{k}(x)-x^{6k}

are roots of unity. Sławomir Biały (talk) 14:45, 8 December 2014 (UTC)[reply]

The connection to cyclotomic polynomials does indeed seem promising, but polynomials of the form

{\frac {x^{n}-1}{x-1}},

from which the former are derived, are not necessarily irreducible. Many times, in fact, they are composite. Hence my dilemma. — 79.118.169.100 (talk) 15:14, 8 December 2014 (UTC)[reply]

I haven't had a chance to look more closely at thus, but here is what I think should happen. The polynominal p_k-1 factors as a product of cyclotomics (and a factor of x or x^2). This tells us that the Galois group of p_k must contain certain commuting cyclic subgroups. I imagine it should be possible to prove irreducibility by studying the inner automorphisms of this subgroup. Combinatorics should play a role. I'd like to be able compute the Gali us groups in a few cases. But computing Galois groups is non-trivial, even for a computer, and I need to remember how to do this in GAP (which I'd the only CAS I have access to capable of handling Galois groups of high order). I'm replying because I don't want this thread to get archived just yet. Sławomir Biały (talk) 18:25, 12 December 2014 (UTC)[reply]

Thank you for your help and continued interest. — 79.113.201.108 (talk) 21:45, 14 December 2014 (UTC)[reply]

FWIW, it's irreducible up to at least

k=600

. -- Meni Rosenfeld (talk) 07:12, 9 December 2014 (UTC)[reply]

Thank you, Meni, for your interest and effort. (You just spared me several hours of CPU time). — 79.114.140.64 (talk) 16:55, 9 December 2014 (UTC)[reply]

Don't thank me, thank my silicon overlord. By the way, the calculation is still running, and so far all values up to 790 have been verified to be irreducible. -- Meni Rosenfeld (talk) 18:11, 9 December 2014 (UTC)[reply]

Maths question[edit]

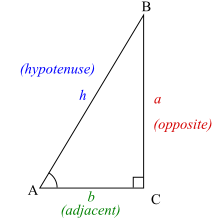
What is cos and tan, and can cos and tan be added together? --Allin Bagsnott (talk) 18:04, 8 December 2014 (UTC)[reply]

See cosine and tangent. cos and tan are mathematical shorthand for these functions, and they are typically used with the angle that you are taking the trigonometric function of, such as cos θ and tan θ for angle θ, or for the diagram on the right, cos A and tan A for angle A. Since they both evaluate to just numbers, yes, they can be added, and in the case of the triangle on the right, cos A + tan A = b/h + a/b. I would say that they are not as natural to add as perhaps sec and tan, where sec is the secant defined as sec A = 1 / cos A. Here, sec A + tan A = h/b + a/b = (h + a)/b which simplified due to the common denominator. We are used to seeing sec and tan added in formulas such as ∫ sec x = ln|sec x + tan x| + C. (See Trigonometric functions#Calculus.) Perhaps someone else here can come up with a common usage of the sum of the cos and tan. -- ToE 20:11, 8 December 2014 (UTC)[reply]

If the question about them being 'added together' is "cos(a+b) = cos(a) + cos(b)" or "tan(a+b) = tan(a) + tan(b)" then the answer is, of course, no. There is, of course, no reason that you can't add the two, ie. "cos(a) + tan(a)" but the result doesn't mean anything particularly significant. It's much more common to see interactions between cos and sin, since they have the useful property cos²(a) + sin²(a) = 1, and it's worth noting that the tangent can be given as tan(a) = sin(a) / cos(a). GoldenRing (talk) 03:52, 9 December 2014 (UTC)[reply]

See List of trigonometric identities#Angle sum and difference identities for actual values of cos(a+b) and tan(a+b). -- ToE 10:06, 9 December 2014 (UTC)[reply]

costan is an anagram for Sno-Cat. So it is clearly meaningful to subtract them, but only after rearranging the letters. Sławomir Biały (talk) 14:18, 9 December 2014 (UTC)[reply]

Is there a special name given to the number between twin primes?[edit]

And also, is there a special name given to the larger of the 2 primes?
It seems that only the smaller of the 2 primes is given a special name (Chen prime). 175.156.91.156 (talk) 23:07, 8 December 2014 (UTC)[reply]

None of them are named. oeis:A001359 only says "Lesser of twin primes". oeis:A006512 says "Greater of twin primes". oeis:A014574 says "Average of twin prime pairs." No alternative names are mentioned except the uncommon "single (or isolated) composites" for the last. Those terms don't appear to be used outside OEIS. Note that a Chen prime is a prime p such that p+2 is either a prime or a product of two primes, so a Chen prime doesn't have to be a twin prime. I wrote http://mathworld.wolfram.com/ChenPrime.html so I should know. PrimeHunter (talk) 23:27, 8 December 2014 (UTC)[reply]

Oh ok, so "Lesser of twin primes" is just a subset of Chen primes. Thanks for the help!
I wonder why the 3 numbers involved in a twin prime (which must satisfy the form 6n-1, 6n, 6n+1 respectively) haven't been given a special name that's less cumbersome than 4 words long.