User:FactSpewer/Draft of Complex Logarithm

The complex logarithm drawn with a color map

In complex analysis, a complex logarithm function is an inverse of (a piece of) the complex exponential function, just as the natural logarithm ln x for positive real numbers x is the inverse of the real exponential function e^x. A complex logarithm is often denoted log z, though care is required to give this notation an unambiguous meaning. Complex logarithms arise in the solution of equations involving the complex exponential function, in the definition of exponentiation when the base is a complex number, in the application of conformal mapping to differential equations, in complex integration, and in many other situations within mathematics, science, and engineering.

Definition

A logarithm of a complex number z is a complex number w such that e^w = z.

• If z = 0, then there is no such w.
• If z ≠ 0, then there are infinitely many w, any two of which differ by an integer multiple of 2πi. For example, the logarithms of i are the numbers πi/2 + 2πin, where n is an arbitrary integer.

Principal value

The principal value Log z defined below is a particular choice of logarithm of z, for z ≠ 0.

Every nonzero complex number z can be written in polar form, $re^{i\theta }$, where r is a positive real number and θ is a real number. Here r is uniquely determined by z, and θ is determined up to addition of an integer multiple of 2π : namely, r must be the absolute value of z, and θ must be a value of the argument of z, i.e., the radian measure of an angle by which one must rotate r counterclockwise in the complex plane to reach z. The unique choice of θ in the interval (−π,π ] is called the principal value of the argument, and is denoted Arg z.

If $z=re^{i\theta }$, where r > 0 and $\theta \in (-\pi ,\pi ]$, and ln is the natural logarithm function on positive real numbers, then the complex number

${\text{Log }}z:={\text{ln }}r+i\theta =\ln |z|+i{\text{Arg }}z$

is a logarithm of z, called the principal value of the logarithm.

Comments about notation

• The natural logarithm of a positive real number x is denoted either ln x (more common in calculus texts) or log x (more common in higher mathematics). For a logarithm of a complex number, the notation log z is usually preferred.
• Some authors use the notation Log z as above to distinguish the principal value from other values of log z.
• Some authors use the convention that log z denotes the principal value unless some other specific branch has been specified.
• Other authors use log z to denote any possible logarithm of z. But careless use of this in equations can lead to meaningless statements.

Properties

• The function Log z is not defined at 0.
• The function Log z is defined but discontinuous at each negative real number.
• When z is a positive real number, Log z agrees with the real analysis definition of ln z.
• By definition, e^Log z = z for any nonzero complex number z.

Common pitfalls

• The identity Log e^z = z fails whenever the imaginary part of z lies outside (−π, π ].
• In particular, given e^z = e^w, one cannot always "take logs of both sides" to obtain z = w.
• The identity ${\text{Log }}z_{1}z_{2}={\text{Log }}z_{1}+{\text{Log }}z_{2}$ can fail: the two sides can differ by an integer multiple of 2πi.

Branches of the complex logarithm

A branch of log z is a continuous function L(z) defined on a connected open subset U of the complex plane such that L(z) is a logarithm of z for each z in U.

Examples:

• The principal branch of log z is the function Log z restricted to the set obtained by removing 0 and all negative real numbers from the complex plane.
• The function Log z + 2πi defines another branch on the same open set.
• The Mercator series

$\log(1+z)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}z^{n}=z-{\frac {z^{2}}{2}}+{\frac {z^{3}}{3}}-\cdots \,$

converges for |z| < 1 and defines a branch of log z on the open disk of radius 1 centered at 1. One can extend this branch to larger regions of the plane by analytic continuation.

There is no branch defined on the entire complex plane, even if one removes 0. Typically, U is chosen as the complement of a ray or curve in the complex plane going from 0 (inclusive) to infinity in some direction. In this case, the curve is known as a branch cut. If the function L(z) is extended to be defined at a point of the branch cut, it will necessarily be discontinuous there; at best it will be continuous "on one side", like Log z.

Once a branch is fixed, it may be denoted "log z" if no confusion can result. Different branches can give different values for the logarithm of a particular complex number, however, so a branch must be fixed in advance (or else the principal branch must be understood) in order for "log z" to have a precise unambiguous meaning.

The complex logarithm as a holomorphic function

If L(z) is a branch of log z on U as above, then L(z) is holomorphic (i.e., complex differentiable) at each point of U, and L′(z) = 1/z.

The complex logarithm as a conformal mapping

The circles Re(Log z) = constant and the rays Im(Log z) = constant in the complex z-plane.

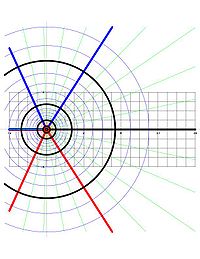
Since any branch of log z is holomorphic with a nonvanishing derivative, it defines a conformal mapping; i.e., it preserves angles of incidence formed by two intersecting curves.

For example, the principal branch w = Log z has the following properties:

• Circles in the z-plane centered at 0 are mapped to vertical segments in the w-plane, connecting a − πi to a + πi, where a is a real number depending on the radius of the circle.
• Rays emanating from 0 in the z-plane are mapped to horizontal lines in the w-plane.

The fact that Log maps the perpendicular intersection of a circle and ray in the z-plane as above to the perpendicular intersection of a vertical segment and horizontal line in the w-plane illustrates the conformal property.

Constructing branches via contour integration

If U is a simply connected open subset of the complex plane not containing 0, then a branch of log z defined on U can be constructed by choosing a starting point a in U, choosing a logarithm b of a, and defining

$L(z):=b+\int _{a}^{z}{\frac {1}{w}}\,dw.$

for each z in U. The complex integral is independent of the path from a to z because 1/w is holomorphic in U and U is simply connected.

The Riemann surface of the complex logarithm

A visualization of the Riemann surface of log z. The surface appears to spiral around a vertical line corresponding to the origin of the complex plane. The actual surface extends arbitrarily far both horizontally and vertically, but is cut off in this image.

Either directly, or via the process of analytic continuation, which "glues together" all branches of log z, one can construct

• a Riemann surface R covering the punctured complex plane $\mathbf {C} ^{*}$, together with
• a single-valued biholomorphic map $\log \colon R\to \mathbf {C}$ whose inverse followed by the projection $R\to \mathbf {C} ^{*}$ equals the exponential map $\exp \colon \mathbf {C} \to \mathbf {C} ^{*}$.

The points of R should not be thought of as complex numbers, however, so this should not be viewed as a way of defining uniquely the complex logarithm of a nonzero complex number.

Visualizing the Riemann surface

The Riemann surface has infinitely many sheets over $\mathbf {C} ^{*}$, and may be visualized as a corkscrew.

Or it may be visualized as a parking garage with levels indexed by all integers: each time one "drives" counterclockwise around 0, one goes up a level.

The Riemann surface and branches of log z

If V is a connected open subset of R that projects bijectively to a connected open subset U of $\mathbf {C} ^{*}$, then identifying V and U (via the projection) identifies the restriction of log to V with a holomorphic function from U to $\mathbf {C}$, and this function is a branch of log z. Every branch of log z arises in this way.

Applications

• The complex logarithm is needed to define exponentiation in which the base is a complex number. Namely, if a and b are complex numbers with a ≠ 0, one can use the principal value to define a^b = e^b Log a. One can also replace Log a by other logarithms of a to obtain other values of a^b.
• Since the mapping w = Log z transforms circles centered at 0 into vertical straight line segments, it is useful in engineering applications involving an annulus.

Plots of the complex logarithm function (principal branch)

• widths="200px"
• 
  z = Re(Log(x + iy))
• 
• 
• 
  Superposition of the previous three graphs

See also

• Complex argument (continued fraction)
• Inverse trigonometric function
• Logarithm

References

[[Category:Complex analysis]] [[Category:Logarithms]] [[fr:Logarithme complexe]] [[it:Logaritmo complesso]]